Un théorème.
Tout entier naturel possède une écriture binaire, et une seule.
Les chiffres en décimal
Rappelons comment on obtient les chiffres, un à un, d'une écriture décimale sur un exemple.
Exemple : les chiffres du nombre 8753.
-
8753 = 875\( \times \)10 +3.
3 (chiffre des unités) est donc le reste dans la division euclidienne de 8753 par 10, et 875 (nombre de dizaines) en est le quotient. -
Nous pouvons réitérer la remarque sur 875 :
875 = 87\( \times \)10 +5.
5 (chiffre des dizaines) est donc le reste de la division euclidienne de 875 par 10 et 87 (nombre de centaines) en est le reste. -
On recommence avec 87 : 87 = 8 \( \times \)10 +7.
7 (chiffre des centaines) est donc le reste de la division euclidienne de 87 par 10 et 8 (nombre des milliers) en est le reste. -
On termine avec 8 : 8 = 0 \( \times \)10 +8.
8 (chiffre des milliers) est le reste de la division euclidienne de 8 par 10. Et le quotient (nombre des dizaines de milliers) est 0.
Ayant obtenu ce 0, nous pouvons stopper la démarche.
Nous avons ainsi explicité un algorithme (appelé algorithme des divisions en cascade) prenant en entrée un entier et donnant en sortie la liste des chiffres de l'écriture décimale (en commençant par le chiffre des unités) de cet entier.
La présentation suivante résumant la démarche justifie le nom
de "divisions en cascade" donné à cet algorithme:
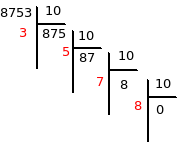
On traduit facilement la démarche précédente à l'aide d'une boucle "Tant que" :
Entrée : un entier n.
Traitement : a ← n
tant_que a est non nul :
r ← reste de la division de a par 10
a ← quotient de la division de a par 10
fin_tant_que
Sortie : les valeurs successives de r
Du décimal au binaire
En remplaçant 10 par 2 dans l'algorithme des divisions en cascade, nous obtenons une méthode d'écriture binaire d'un entier naturel.
Entrée : un entier n.
Traitement : a ← n
tant_que a est non nul :
r ← reste de la division de a par 2
a ← quotient de la division de a par 2
fin_tant_que
Sortie : les valeurs successives de r
Exemple : obtenir les chiffres de l'écriture binaire de 13.
a=13 et a=2*6+1. Le bit de rang 0 (bit de poids \( 2^0 \) ) est donc 1.
a=6. a=2*3+0. Le bit de rang 1 (bit de poids \( 2^1 \) ) est 0.
a=3. a=2*1+1. Le bit de rang 2 (bit de poids \( 2^2 \) ) est 1.
a=1. a=2*0+1. Le chiffre de rang 3 (bit de poids \( 2^3 \) ) est 1.
a=0. On a terminé.
L'écriture binaire de 13 est donc 1101binaire.
De façon plus lisible :
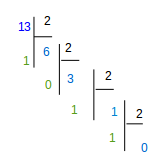
Les chiffres bleus sont les valeurs de a successives dans le déroulement de l'algorithme (la valeur 0 marque l'arrêt
de l'algorithme). Les chiffres verts sont les restes successifs, celui du haut étant celui qui sera à droite dans l'écriture
binaire, celui du bas sera le plus à gauche dans l'écriture binaire.
Chiffre de poids faible, chiffre de poids fort
Dans l'écriture en base b=10 ou en base b=2, on appelle poids d'un chiffre la puissance de b correspondante.
Exemple. 8753= 8\( \times \) 103 + 7\( \times \)102 + 5 \( \times \) 101 +3\( \times \)100 : le poids de 3 est 100, le poids de 5 est 101, le poids de 7 est 102 et le poids de 8 est 103. Le chiffre 3 (chiffre des unités du nombre 8753) est appelé chiffre de poids le plus faible (ou même souvent chiffre de poids faible) . Le chiffre 8 est le chiffre de poids le plus fort (souvent appelé chiffre de poids fort).
De même dans 1101binaire, le 1 écrit à gauche est le chiffre (on dira plutôt le bit en base deux) de poids le plus fort (ici de poids 23) ou MSB (most significant bit), et le 1 de droite est le bit de poids le plus faible (de poids 20) ou LSB (lowest significant bit).
On fera attention au fait que l'algorithme présenté ci-dessus donne les chiffres dans l'ordre croissant des poids (poids le plus faible en premier, poids le plus fort en dernier) alors que l'on écrit ensuite le nombre de gauche à droite en commençant par écrire les chiffres de poids forts.
Passer de la base 10 à la base 2.
L'exemple précédent a montré comment passer d'une écriture décimale à une écriture binaire. Exercez-vous.